내 태그

입시

학습

생활

클럽

직업·취업

Epioptimus

Centurion

오르비 랭킹

XDK 누적 복권

XDK 경매

RARE

leenie [1221169] · MS 2023 · 쪽지

2024-07-09 22:37:09
조회수 12,694
2

소소한 시험 꿀팁 + [과천중앙고] 2024년 1학년 1학기 기말고사 손풀이

게시글 주소: https://roomie.orbi.kr/00068684321

(100.0K) [362]

2024 과천중앙고 1학년 1학기 기말고사 (수학).pdf

안녕하세요. 수학의 판도를 바꾸는 Math Changer 어수강 박사 (과천 "어수강 수학" 원장)입니다.

오늘은

[과천중앙고] 2024년 1학년 1학기 기말고사 손풀이

포스팅 하도록 하겠습니다^^

PS. 시험 꿀팁은 본문 마지막에 있습니다 :)

[원문 출처] https://blog.naver.com/math-fish/223507228348

학생이라면 풀이를 보기 전에 문제를 풀어볼 것을 강력하게 권장합니다.

1-2페이지는 무척 쉽네요 ㅎㅎ

3 페이지도 어느 정도 공부를 했다면 무난히 풀 수 있는 문제들로 구성되어 있습니다.

10번 문항은 미지수가 a, b 두 개니까 식도 2개가 필요하겠죠? 거리 조건 + 무게 중심의 좌표를 이용해서 식을 세우면 끝입니다.

11번은 복이차식이므로 이차항을 t로 치환하면 되겠죠? 이때, x가 서로 다른 네 실수가 된다는 것을 t에 대한 필요충분조건으로 바꿔야 한다는 사실에 주의해야 합니다!

12번 문제는 근을 모르므로 문자로 세팅하면 되겠죠? 그럼 미지수가 3개이므로 근과 계수의 관계를 이용해서 식도 3개를 세우면 무난하게 풀 수 있을거라 생각합니다.

구체적인 풀이는 다음과 같습니다.

이제 4페이지를 살펴볼께요!

13번 문제는 연립부등식 문제이므로 하나씩 풀면 되겠죠? 당연히 정보가 많은 이차부등식부터 풀어야 합니다. 그리고 일차부등식의 해집합을 수직선 상에 나타내면 되겠죠? 이때 k의 값이 변해도 해집합(닫힌 구간)의 길이가 10으로 변하지 않는다는 사실에 초점을 맞추고, 해집합을 좌우로 움직여가며 언제 주어진 조건이 만족되는지 확인하면 됩니다!

14번 문제는 ㄴ, ㄷ에서 등식을 k에 대한 항등식으로 생각하고 풀면 쉽게 풀 수 있습니다.

16번은 삼차연립방정식이므로 차수를 낮추거나 미지수 개수를 줄이면 되겠죠? 여기서는 차수를 낮추는게 좋아보이네요! (미지수를 쉽게 없앨 수 없고, 차수는 쉽게 낮출 수 있으므로!)

다음 풀이에서와 같이 차수를 낮추면, 공통근을 바로 알 수 있으므로 이를 이용하여 문자수를 줄여주면 무난하게 풀 수 있습니다.

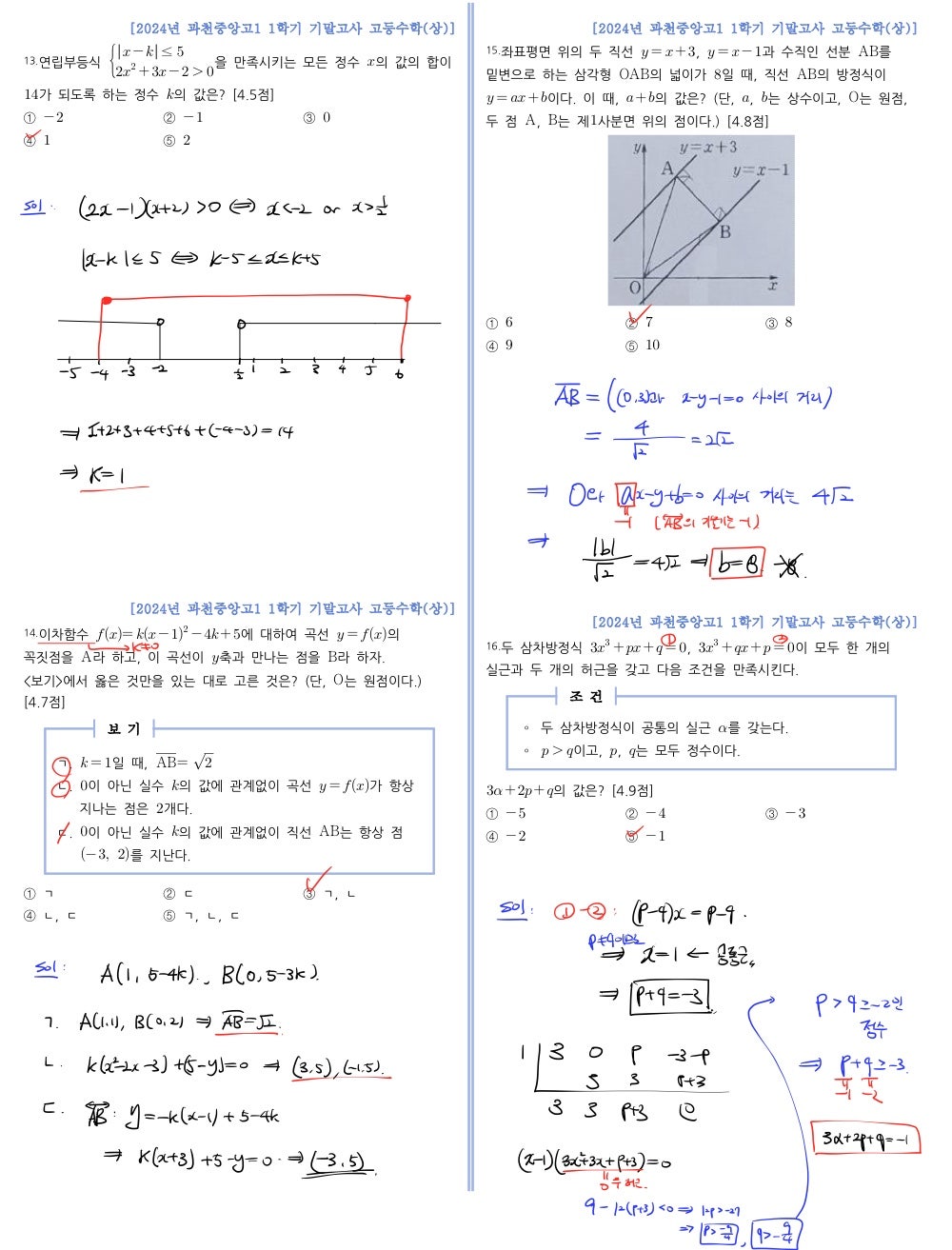
이제 5페이지를 볼게요!

17번 문항은 삼각부등식을 이용하면 쉽습니다. 보통은 B(-6, 8)과 같이 주고, 이를 y축에 대칭이동시켜야 풀 수 있는 문제를 출제하는데, 시험 범위에 대칭이동이 들어가지 않기 때문에 오히려 쉽게 출제된 것 같네요.

18번 문항은 보기엔 어려워 보이지만 삼단논법으로 풀면 차근차근 풀면 쉽게 풀 수 있습니다.

1. 먼저 A, B의 좌표를 구해야 겠죠?

2. 세 변 중 어떤 두 변의 길이가 같은지 모르니 경우를 나누어야겠죠?

3. 각각의 경우를 식으로 나타내면 끝!

19번 문항은 차수를 낮추는데 초점을 맞추면 아주 쉽습니다!

20번 문항은 평소에 평행선만 가지고 문제를 풀었다면~ 최댓값을 구하지 못하거나, 시간을 많이 뺏길 가능성이 높습니다. 반면, 다음 풀이와 같이 주어진 조건을 식으로 세워서 푸는 연습을 한 학생이라면 무난히 풀 가능성이 높습니다!

이와 같이 유연하게 대처하려면, 평소에 "삼단논법"을 통해, "배운 것에 근거"해서 "여러 가지 방법"으로 풀어보는 것이 중요하겠죠?

이제 마지막 페이지를 볼까요?

21번은 무척 어려워보이지만, 풀이가 조금 길 뿐이지 사실 무척 쉽습니다. 풀이 아이디어는 다음과 같습니다.

1. (가), (나)로부터 다음 풀이와 같이 인수정리 사용하면 f(x), g(x)를 k에 대한 식으로 단번에 나타낼 수 있겠죠?

2. 이차부등식이 항상 성립한다는 조건으로부터 판별식을 쓰면 k에 대한 부등식이 나오겠죠? 이걸 풀면 끝입니다.

이와 같이 주어진 조건으로부터 할 수 있는 것이 무엇인지, 또는 원하는 것을 얻기 위해 필요한 것이 무엇인지, 차근차근 풀면 쉽게 풀 수 있겠죠? 이와 같이 어려워보이는 문제도 쉽게 풀 수 있는 힘!! 이것이 삼단논법의 강력한 점이겠죠? ㅎㅎ

벌써 마지막 문제네요. 22번 또한 삼단논법으로 차근차근 생각해 볼게요!

1. 삼각형의 세 변, 세 각, 그리고 이차함수가 등장하네요! 이중 정보가 가장 많은 것에서 출발합시다!!!

이때, 미지수가 2개이므로 식도 2개 이상 필요하다는 것과, 두 개를 동시에 하기 어려운 경우 하나씩 생각하는 것을 알면 좋겠죠?

2. 세 각의 크기는 모두 알고, 세 변 중에서는 BC만 완벽히 알고 있죠? 왜냐하면 (1, 0)을 지나는 기울기가 root 3인 직선이니까요!!

3. 직선 BC의 방정식을 이용해서 a, b 중 무엇을 알아낼 수 있는지 생각해 보세요! 접한다는 조건을 이용하면 단 번에 b를 알아낼 수 있습니다 :)

그럼 이제 무엇을 이용해야 a의 값을 구할 수 있을까요?

4. a의 값을 구하려면 a에 대한 식을 세워야겠죠? 삼각형의 각 꼭짓점을 a에 대한 식으로 나타내고~ 이를 이용하여 등식을 세울 수 있는지 생각해 보면 P가 이차함수 위의 점이란 것을 이용하면 된다는 것을 쉽게 알 수 있겠네요!

구체적인 풀이는 다음과 같습니다.

지금까지

[과천중앙고] 2024년 1학년 1학기 기말고사 손풀이

를 알아보았습니다. 문제가 깔끔하고 구성도 좋아보이네요!

문제를 유형화해서 기계적으로 푸는 학생들에겐 16번, 18번, 20번, 21번, 22번의 체감난도가 꽤 높았을 것 같네요. 상당수가 시간만 뺏기고 답을 내지 못했을 것 같습니다. 반면, 배운 것에 근거해서 문제를 분석하고, 삼단논법을 통해 논리적으로 문제를 해결하는 학생들에겐 무난했을거라 생각합니다.

기계적으로 공부하지 말고, 하나하나 정확하게 공부하세요. 최소한 "무엇을?", "어떻게?", "왜?" 하는지 고민하며 공부하기 바랍니다. 이와 같이 공부한다면 안정적인 1-2등급도 별로 어렵지 않을테니까요 :)

PS. 똑같은 실력이라도 시험 전략에 따라 많게는 20점 이상 차이가 나기도 합니다. 앞에서 몇 문제가 잘 안풀려서 시간을 뺏기고 풀지 못하면, 마음이 급해져서 문제가 눈에 들어오지 않고, 이렇게 되면 충분히 풀 수 있는 문제도 제대로 풀지 못해서 시험을 망치는 경우가 많습니다. 따라서 다음과 같은 전략을 추천합니다.

STEP1. 시험지를 받으면 가장 먼저 문항 구성 및 배점을 살펴본다.

STEP 2. 풀 수 있는 것들 먼저 정확하게 풀고 안 풀리는 문제는 쿨하게 넘어갑니다. 처음부터 문제 풀이 방향을 잘못 잡았거나, 계산을 틀린 경우, 계속 보고 있는다고 해서 틀린 것이 잘 보이지 않는 경우가 많습니다. 안 풀리는 것은 쿨하게 넘어감으로써 시간을 절약하고, 차후에 다시 돌아와서 차근차근 분석해서 풀면 틀린 것이 보일 가능성이 훨씬 높기 때문입니다.

STEP 3. 다시 처음으로 돌아와서 풀지 못한 문제를 차근차근 분석해서 풉니다.

과천중앙고 시험 문제를 예로 위 전략에 대해 설명하면 다음과 같습니다.

STEP 1. 시험지를 전체적으로 살펴보면 객관식 17번, 18번보다 논술형 1번, 2번, 3번이 훨씬 쉽고 배점이 크다는 것을 알 수 있습니다. (공부를 제대로 한 학생이라면 알 수 있지만, 공부를 하지 않은 학생은 알 수 없습니다^^;;)

STEP 2. 만약 저였다면, 17번, 18번이 잘 풀리지 않는 경우, 쿨하게 넘기고 논술형 1번, 2번, 3번을 먼저 풀 것입니다.

17번, 18번에 시간 투자를 했는데 풀지 못하면 0점이지만, 17번, 18번을 쿨하게 넘기고 논술형 1번, 2번, 3번 중에 2개는 풀고, 1개는 부분점수만 받아도 15점 이상 차이가 날 수 있습니다.

STEP 3. 17번, 18번과 같은 문제에서 시간을 뺏기지 않았기 때문에, 다시 돌아와서 풀 수 있는 시간이 남았을 가능성이 높습니다. 이때, 본문의 풀이에서처럼 차근차근 분석해서 풀면 됩니다.

[원문 출처] https://blog.naver.com/math-fish/223507228348

다음은 공부에 도움이 될 만한 링크입니다.

1. 거의 모든 고난도 문항에 즉각 적용 가능한 치트키 1 : https://orbi.kr/00062136893

2. 거의 모든 고난도 문항에 즉각 적용 가능한 치트키 2 : https://orbi.kr/00062194726

3. 문자의 개수 vs 식의 개수 (feat. 연세대) : https://orbi.kr/00064497772